Page Contents
… simply explained
The resolving power or resolution of a lens refers to its ability to capture fine details in a subject and reproduce them sharply in an image. The higher the resolving power, the more detail and sharpness the lens can deliver.
What is the difference between resolution and sharpness?
Resolution refers to the level of detail in an image. The higher the resolution, the more details can be displayed. You can think of it like a mosaic: the more small tiles the mosaic has, the more detailed the image. Sharpness, on the other hand, describes the precision with which the transitions between light and dark areas of an image are displayed. A sharp image shows clear, defined edges and contours.
The resolution contributes to the impression of sharpness, but is only one of several elements, see.
How is Resolving Power Measured?
The resolution is usually measured by looking at lines next to each other.
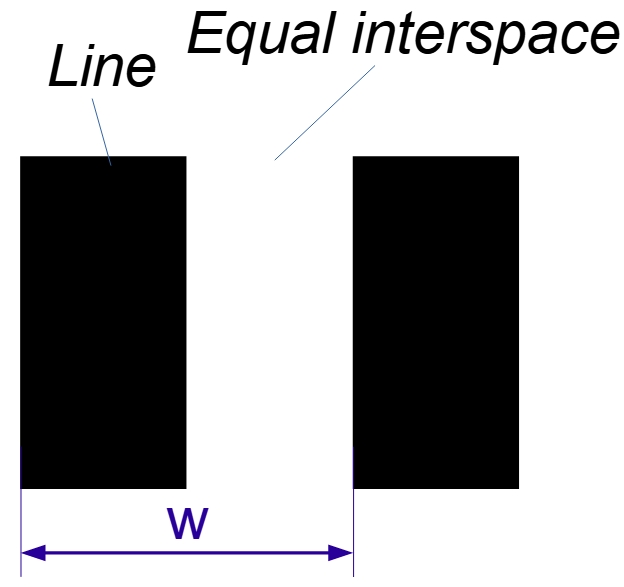
The lens defects or the film grain cause the sharp, high-contrast lines of the test pattern to fade into gray tones. You then vary the distances and look for the distance w at which you can just distinguish between two neighboring lines. The resolution limit is reached at the line pair that is so close together that the resulting gray lines just touch each other:

The distance w between the lines, at which the lines can just be distinguished from each other, is a measure of the resolution. More precisely, w is a measure of the weakness of the resolution. This is because the greater the distance w, the weaker the resolution.
The unit of the distance w is mm per line pair (mm/LP). Assume that the distance w is 0.1 mm. Then 10 line pairs would fit on 1 mm. This would then be the resolution r. The unit of resolution would therefore be line pairs per mm (LP/mm). In our example
r = 10 LP/mm
The resolution r is therefore the reciprocal of the resolution weakness w:
r = 1/w = 1/(0.1 mm/LP) =10 LP/mm
The resolution indicates the number of alternating black and white lines of high contrast that we can still distinguish per millimeter. The higher the value, the better the resolution.
Single resolution and system resolution
So far we have looked at the resolution of a single component. Such a component could be our eye, a camera lens or a film. However, we are often not only interested in the resolution of a single component, but the resolution of an entire system. Such a system could be an analog camera, consisting of a lens and film. Assuming I know the resolution of the lens and the film, what is the resolution of the camera? Is the system resolution equal to the lower or higher value of one the two components?
Neither. As you can easily imagine, the overall resolution will be worse than any of the components involved, because each component affects the overall result. Suppose we know that our lens has a resolution of rLens = 10 LP/mm and the film has a resolution of rFilm = 20 LP/mm. Let’s take a concrete look at what happens to the system.
We start with the lens. With a resolution of 10 LP/mm, the lines repeat at a distance of
wLens = 1 / rLens = 1 / 10 = 0.1 mm
The distance between two lines is wLens / 2 = 0.05 mm.
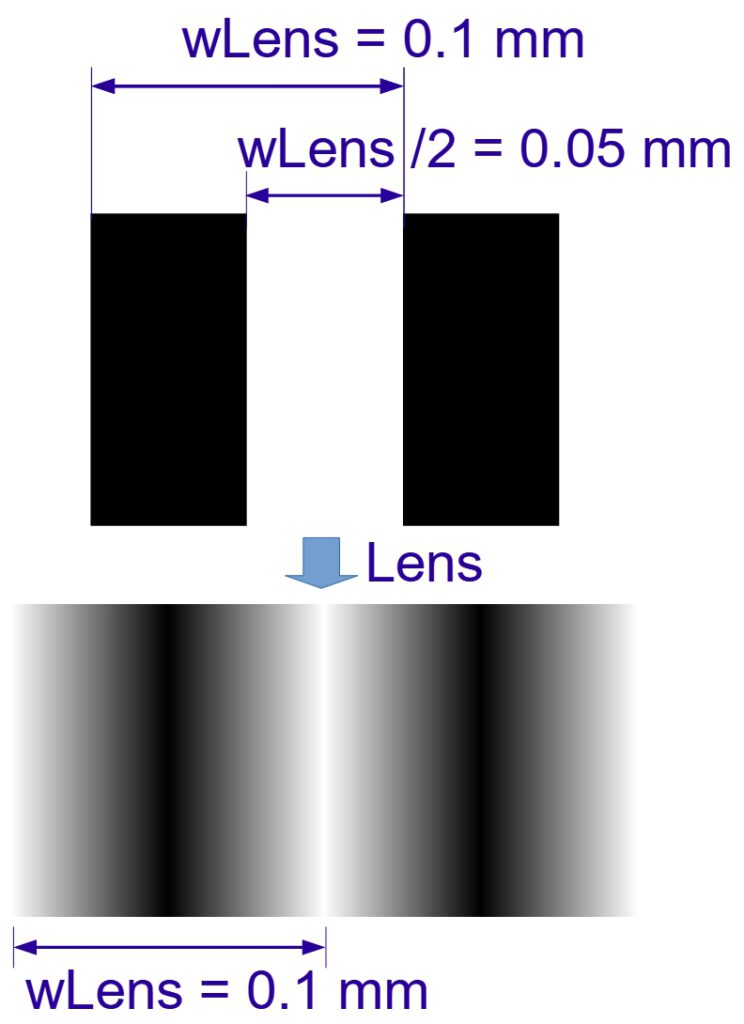
The lines created behind the lens have a gray gradient and meet directly. You can see immediately that the two resulting lines each have a width of wLens = 0.1 mm.
Now we come to the second component, the film. The film is not hit by the original test pattern but by line pairs from the lens of the width wLens. Because of the film’s resolution of 20 LP/mm, the distance between the incoming lines is
wFilm /2 = 1/rFilm / 2 = 1/20 / 2 = 0.025 mm
However, the incoming lines themselves have the width wLens:
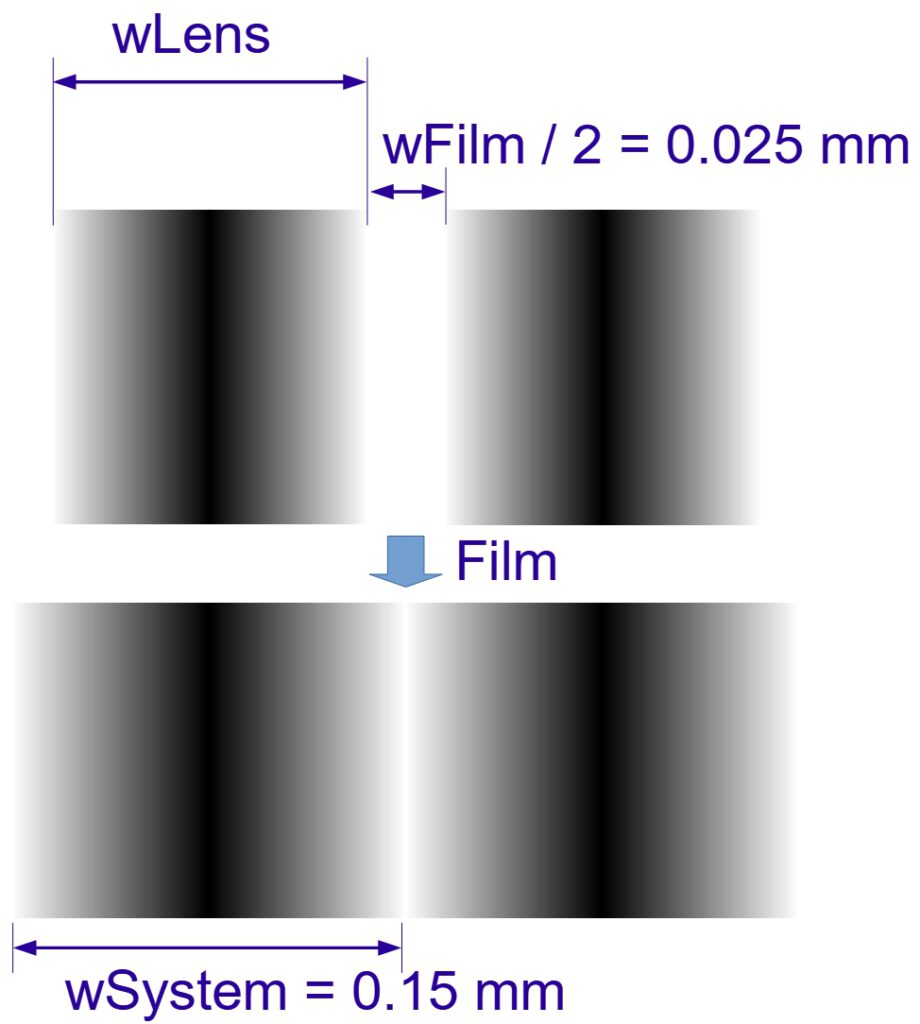
This results in an overall resolution weakness due to the lens and film
wSystem = wLens + wFilm = 0.1 mm + 0.05 mm = 0.15 mm
The overall resolution of the system is then
rSystem = 1 / wSystem = 1 / 0.15 = 6.67 LP/mm or by using r = 1/ w:
rSystem = 1 / wSystem = 1 / (wLens + wFilm)
rSystem = 1 / (1 / rLens + 1 / rFilm) or 1 / rSystem = 1 / rLens + 1 / rFilm
rSystem = 1 / (1/10 LP/mm + 1 / 20 LP/mm) = 6.67 LP/mm
This is the derivation of the equation which is also given by FujiFilm in the “Professional Data Guide”, 2005, page 129 in the section “Resolving Power”.
Back-calculating resolutions
Sometimes you have the overall resolution of the system and want to know the resolution of a component. Suppose we had photographed a test pattern with an analog camera and determined the total resolution from the negative. Further assuming we knew the resolution of the film, we could calculate the aerial resolution of the lens. Above we have learned
1 / rSystem = 1 / rLens + 1 / rFilm
→ 1 / rLens = 1 / rSystem – 1 / rFilm
→ rLens = 1 / (1 / rSystem – 1 / rFilm)
Using the values from the example above, we obtain
rLens = 1 / (1 / 6.67 – 1 / 20) = 10 LP/mm
Conclusion
We have seen that the resolving power of a system can never exceed the lowest resolving power among the components that comprise the system. In fact, the system value is actually lower.
We have derived a formula that describes how to calculate the total resolution of a system consisting of several components. For this purpose, we have introduced a new parameter, namely the weakness of the resolution as the reciprocal of the resolution.
Thanks to Martin, who had the idea to introduce the weakness of the resolution instead of calculating with the reciprocals of the Fujifilm equation.
